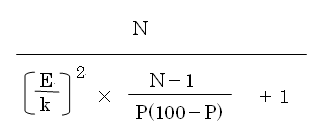
E = 許容できる誤差の範囲
P = 想定する調査結果=50(%)
(50%のときに最大のサンプル数となるため)
k = 信頼度係数=1.96
(通常,信頼度95%を基準とするため)
医学における統計処理の問題点を考える前に,ちょっと別の各度から統計処理について述べてみたい。
ご存知の方はご存知と思うが,各種の世論調査はどれも1500~2000人を対象に行っている。そしてなぜか,5000人を対象とした世論調査も,8000人で調べた世論調査も存在しない(はずである)。1億人の意見を調べようとすれば2000人の意見を調べたらもうそれで十分だかららしい。さらに言うと,10万人の意見を調べるのも2000人で十分なのである。
なぜ2000人でいいかと言うと,そういう計算式と言うか統計処理方法があるからである。これに基づくと,1万人の世論調査に必要なサンプリング数は1300人ほど,10万人で1500人ほどであり,それ以上はいくら母集団が増えてもサンプリング数は1500でよいと言う結果になる。
必要なサンプル数を算出する根拠となっている数式は次の通りである(出典は2004年に出版された雑誌「サイゾー」のコラム記事。その雑誌は手元にないため,雑誌号数は不明)。
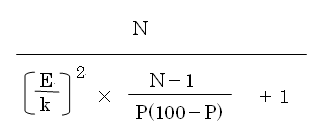 |
N = 全体の人数(母集団) E = 許容できる誤差の範囲 P = 想定する調査結果=50(%) (50%のときに最大のサンプル数となるため) k = 信頼度係数=1.96 (通常,信頼度95%を基準とするため) |
これを元に素直に計算してみると,確かに上記のような「10万人以上の集団の世論調査には1500ほどで十分,2000人調べたらお釣りがくる」事がわかる。要するに,母集団の数を増やせば増やすほど,1537に近づくのである。2000人だったら多すぎるほどである。
| N(母集団の数) | 必要なサンプル数 |
| 2 | 2 |
| 100 | 94 |
| 1,000 | 607 |
| 100,000 | 1,514 |
| 10,000,000 | 1,537 |
| 1,000,000,000 | 1,537 |
上記の数式で使われている変数は4つだけだ。このうち,感覚的にも理解できるのはN(母集団の数)だけだ。だが,残りの3つの変数が何ともいかがわしい。
E(誤差範囲)はいいだろう。これをまず決めておかないと,話が進まない。
P(想定する調査結果)と言うのは何だ? 何で初めから50%に決めておくんだろう? それなら,最初から変数でなく定数にしておけばいいのに・・・。
k(信頼度係数=1.96)というのも信頼度を最初から95%にしておくのなら,これも定数じゃないのか?
上記の「10万人以上の集団なら1500人を調査すればいい」と言う数字は,E = 2.5にした時の数字である。試しにE = 1にしてみると1000人の集団ではサンプル数は835人ほど,10万人では8772人ほどになるはずだ(久しぶりの筆算なんで,間違っている可能性が大きいけれど)。
要するに,誤差をちょっと変えるだけで,サンプリング数は驚くほど大きく変わってくる。また,P = 50としているため P(100 - P) = 2500 であり,(N-1)/P(100-P) は N の値で一義的に決まってしまう。
ちなみに,P の値を変えてみると P(100-P) の値は次のようになる。
| P | P(100-P) |
| 1 | 99 |
| 10 | 900 |
| 30 | 2100 |
| 50 | 2500 |
| 70 | 2100 |
| 90 | 900 |
| 99 | 99 |
ということで,上記の式を眺めていれば,N の値が大きくなれば P(100-P) の影響はどんどん小さくなり,式の値が一つの上限値にどんどん近づくことが予想されるはずだ。
というわけで,サンプリング数を決めるのは上記の式のE(誤差範囲)の取り方一つだということがわかる。このEの値で,上記のサンプリング数はある値に収束するのである。
Eの値をちょっと大きくすれば「どんな大集団の世論調査でも少ないサンプリング数で十分」となり,Eをちょっと小さくすればすぐに「莫大な数のサンプリング数が必要」になってしまうのだ。「誤差範囲」の2乗に反比例しているのだから当然である。
ここで (E/k)3 とすれば,誤差範囲の数値が及ぼす影響は,さらに大きくなる。
となると,この式の分母にある "+1" の意味がわかってくる。この 1 がなければ,k(信頼度係数)より誤差範囲を小さな値にすると「サンプリング数が母集団より大きくなる」と言うマヌケな状況になってしまうので,それを避けるために 1 を足しているんじゃないだろうか(違うかもしれないけど・・・)。この 1 があるおかげで,誤差範囲の値によらず,「サンプリング数は母集団の数より小さくなる」はずだ。
そうなると今度は,なぜ 1 を足すのか,訳がわからなくなってくる。1.22 でもなく 2.38 でもなく,なぜ 1 なんだろうか。根拠のある 1 なんだろうか。この 1 は 1.0 なんだろうか,1.00 なんだろうか,それとも「大体 1 」なんだろうか。
こうなると,分母にある N - 1 の 1 も怪しくなってくるぞ。なぜ 1 を引くんだろう? なぜ 1 なんだろう。N が一桁の数字ならこの 1 は意味を持つが,二桁以上の数字になるとこの 1 はどんどん影響がなくなっていく(試しに計算してみてください)。1 を引いても引かなくても,サンプリング数には全く影響がない。N の大きさと無関係に 1 だけ引くなんて,いかにも「この数式には裏付けがあるんです」的な何だか姑息なものを感じちゃうのである。
だが現実には,この数式を元に世論調査に必要なサンプリング数が決められ,10万人の集団でも10億人の集団でも,調査すべきは1500~2000人となっているのである。最初から誤差2.5%を想定しているから当然である。
しかも,調べた2000人が母集団の意見を反映するように完全にランダム抽出した2000人だったらいいが,実際には電話調査などの手段が選ばれているため,偏りは避けられないはずだ。要するに「誤差を前提に誤差を重ねる」訳である。
ところがこの数式は統計学的に正統なものらしい。だから,新聞もテレビもその他のマスコミもそれを元に2000人くらいを調査して,「世論はこうなっています」と発表するわけだ。誤差範囲をたまたま 2.5 にしたから,たまたま1500(2000)という数値になっただけで,誤差範囲をちょっと変えるだけで,必要なサンプリング数は大きく変わるのだが,世論調査の結果だけ見ていると,こういうカラクリが見えてこない。
こうなってくると,「世論調査が必要だけど,手抜きしたいんだよ。1000人とか2000人くらいの調査で十分だと言う根拠を与えてくれる適当な数式ってないかなぁ」ということから上記の数式が決まったんじゃないか,と勘繰りたくなってくる(こういうのをゲスの勘繰りっていうんだな)。
統計処理と言うと,いかにも厳密な数学理論と計算によって結果の正誤を判断できる,と信じてしまうが,少なくともこの「世論調査に必要なサンプリング数を求める統計計算」だけはインチキ臭いのである。
こういう数字のカラクリを見てしまうと,新聞紙面に踊る「小泉政権を指示する人の割合は57.2%と過半数を超えており,国民に支持されている事がわかる」なんて記事がなんだかすごく嘘っぽいのである。
(2004/06/21)