黄金比という言葉をご存じだろうか。恐らく数学好きでなくても「ピラミッドに隠された黄金比の秘密」とか,「モナリザの美と黄金比」とか,「パルテノン神殿は黄金比で作られているから美しい」というのはどこかで見かけたことがあると思う。美術以外でも,作曲家のバルトークがリズム分割や楽章構成に黄金比を利用していたというのは音楽マニアの間では有名であるし,バッハやモーツァルトの音楽に黄金比がある,という説明も読んだことがある。そのくらい,美と黄金比の関係は確固たるものとして捉えられている。
しかし本書は,それに異を唱え,本当に黄金比は人の美感に訴えるものなのか,美しいものには黄金比があるのか,今まで黄金比が見つかったとされていたものは本当にそうなのか・・・を厳密に再検討する。そして,本来の数学での黄金比の意味,生物界と宇宙を支配する黄金比の魅力を余すところなく描き出している。
黄金比(φ)は数学の世界では至る所に登場する。その意味では円周率(π)と双璧だろう。黄金比を具体的な数字で書くと
φ = 1.61803339887498948482045868…… という無理数であるが,これがいろいろ面白い。
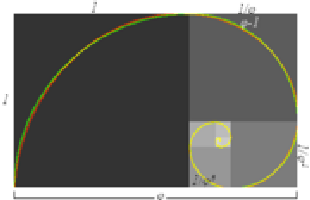
例えば,短辺が1,長辺がφの長方形を書き,その中に一辺の長さが1の正方形を書くと,残ったところにできた長方形の辺の長さの比は 1:φ になっている。つまり,相似の長方形ができる。そして,この小さな長方形の中に正方形を作れば,さらに小さな黄金比の長方形が出現し,これは無限に続く。おまけに,この正方形の頂点をつなぐと美しい螺旋系が出現するが,これはアンモナイトやオウムガイの断面と相似であり,ヒマワリの種の配列であり,銀河系の渦巻き構造に厳密に一致している。

あるいは☆の形もそうだ。一筆書きではこのように書くが,さまざまな辺の比のなかに,幾つもの黄金比が見いだせるのだ。ピタゴラスがこの図形をグループの象徴としたのも,これが無限の黄金比で構成されているからだったという。

あるいはフィボナッチ数列。これは,1, 1, 2, 3, 5, 8, 13 ……, Fn, Fn+1, [Fn + Fn+1], ……という数列で,前の二つの項を足して新しい項を作るという数列だが,この連続した二つの数の比(Fn+1/Fn)を取ると,限りなくφに近づくのだ。また,この数字を正方形の一辺として配列し,頂点を結んでいくと,前述の「アンモナイトの渦巻き」が登場する。
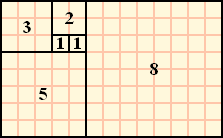
ちなみに,二つの整数(例えば3と148とか)を考え,この二つの数字を足して新しい項とし(この場合は151),さらに148と151を足して新しい項(299)を作り・・・というのを続けていくと,この数列の連続する二つの項の比も限りなくφに近づく。理由は自分で考えようね。
同時にφは非常に美しい連分数でも表されることでも有名だ。
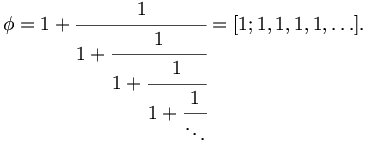
このほかにも,木の枝や草の葉が新たに分岐する角度が,その前に出た枝と 180/φ の角度を取る生物学的な必然性とか,銀河の渦巻き構造が維持されるための数学的条件とか,フラクタルとφの関係とか,話題は広大で興味が尽きない。
一方で,美術でよく言われている「黄金比は美しい」という嘘は容赦なく暴いている。例えば下図は有名な「パルテノン神殿に見られる黄金比」として美術や数学書に引用される図だが,この線の引き方が恣意的で,結局,「黄金比になるように引いた」線に過ぎないことを看破しているのである。たとえば,数の一番外側の長方形では「屋根の先」と柱の基部が境界線になっているが,柱の下の土台はなぜか無視されている。なぜこの土台部分を無視するかというと,ここを入れると黄金比になってくれないからだ。同様に,真ん中辺りの「一番小さい長方形」も,何を基準に描いたのか不明である。

このように,他の絵画や建築で従来指摘されていた黄金比が,実は線の引き方が恣意的で,それらが「無理やり見つけた黄金比」であることを,明確に指摘している。そして,「黄金比を美しく感じるのは人間の自然な感性」とか,「美を求めて黄金比に行き着いた」というのはでっち上げに過ぎないと結論付けている。
「黄金比は美しい」というのを常識だと思ってみると,モナリザにもパルテノン神殿にも東照宮にも黄金比は見つけられるが,「それって本当に正しいの?」という疑いの目で見直すと,実は「黄金比を見つけよう」というバイアスがかかっていただけだったことがわかるのだ。実に痛快である。
(2006/04/19)